 assets/3eLoi_apesanteur.mp4
assets/3eLoi_apesanteur.mp4

 assets/3eLoi_apesanteur.mp4
assets/3eLoi_apesanteur.mp4
La dynamique est la branche de la mécanique qui relie les mouvements à leurs causes : les forces.
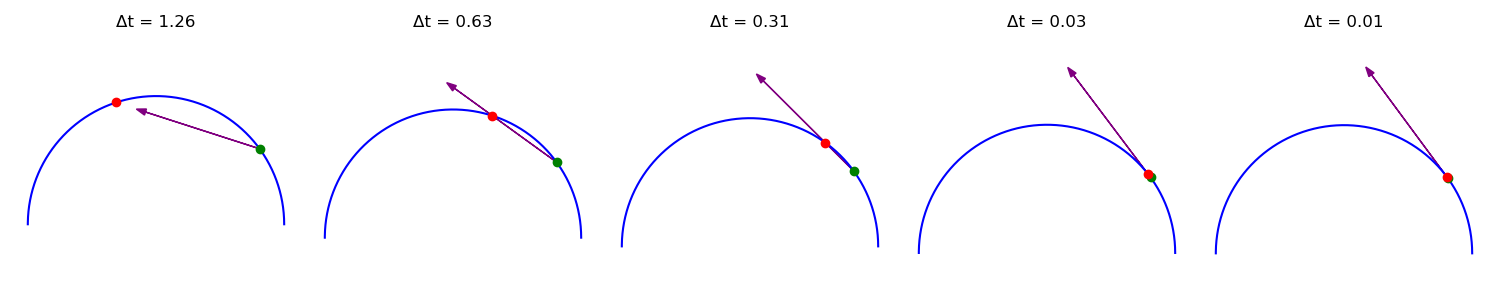
Le vecteur vitesse \(\overrightarrow{v_i}\) représente la vitesse instantanée d’un solide au point \(i\). On s’en approche en calculant la vitesse moyenne sur un tout petit intervalle.
Caractéristiques :
Notation : \(\overrightarrow{v_i}\)
Montrer que l’on fait simplement v = d / t. Parler des deux méthodes (points consécutifs ou méthode centrée)
Calcul : \(\overrightarrow{v_i} = \frac{\overrightarrow{M_{i-1}M}_{i+1}}{2·\Delta t}\)
calcul de vecteur vitesse|\(\overrightarrow{v_i} = \frac{\overrightarrow{M_{i-1}M}_{i+1}}{2·\Delta t}\qquad\frac{distance}{durée}\)
ex 3 p. 224
ex 2 p. 224
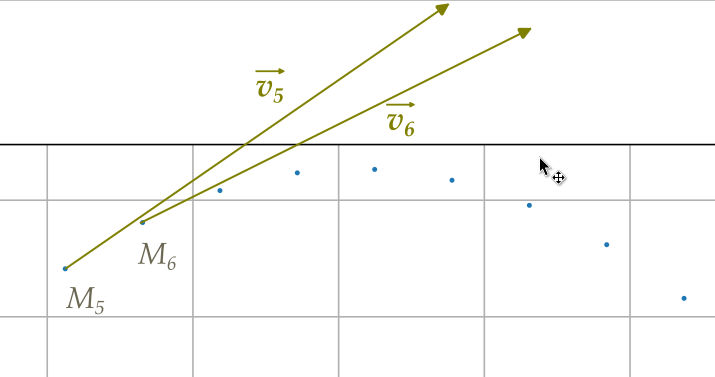
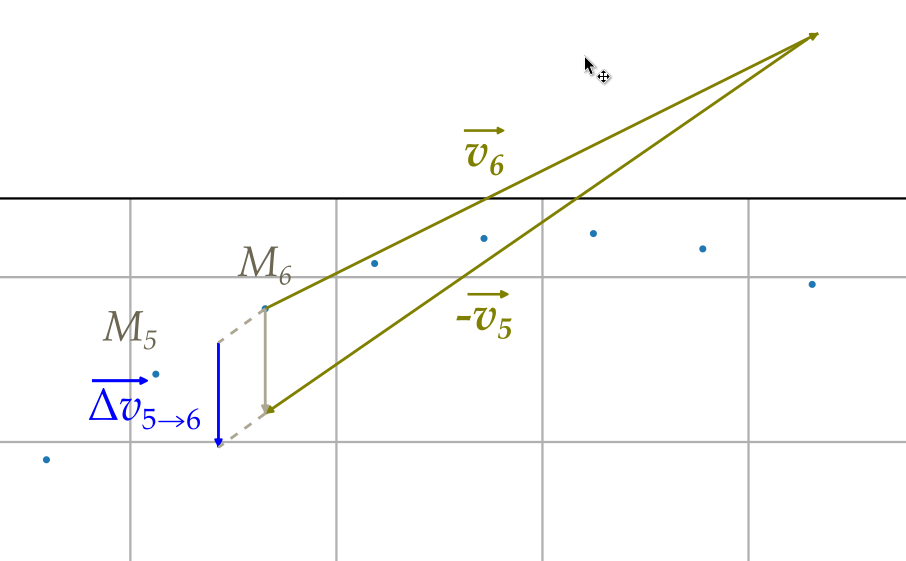
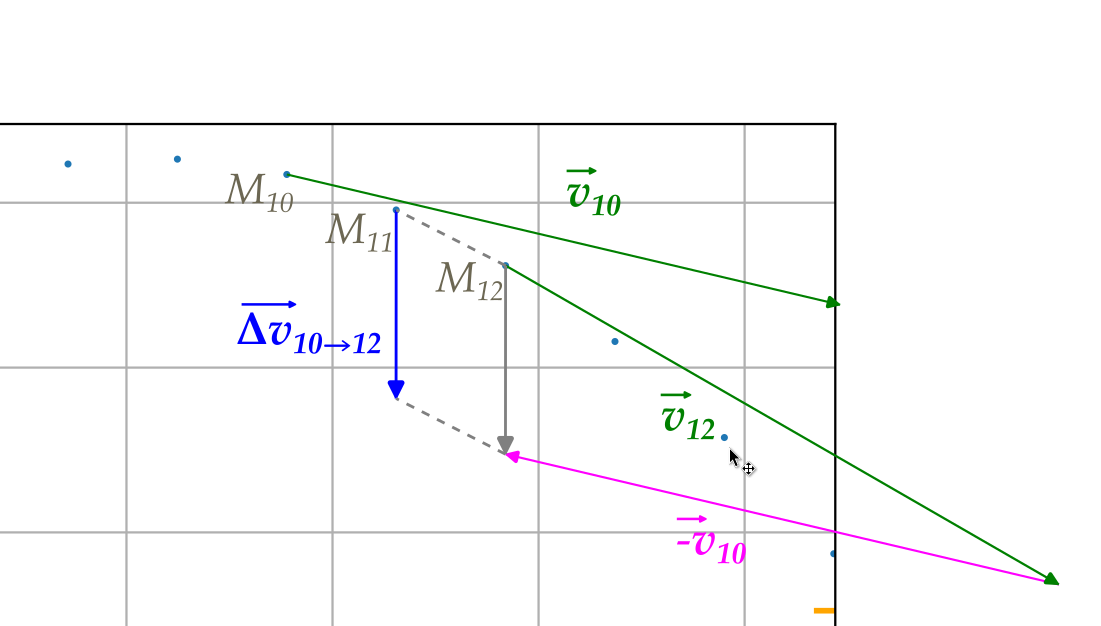
Le vecteur variation de vitesse entre les points \(i\) et \(j\) se note \(\overrightarrow{\Delta v}_{i \rightarrow j}\). On le place généralement entre les points i et j.

\[{\overrightarrow{\Delta v}}_{i \rightarrow i+1} = \overrightarrow{v_{i+1}} - \overrightarrow{v_{i}}\]
Si \(\overrightarrow{v_5} = \begin{pmatrix}3\\7\end{pmatrix}\), et \(\overrightarrow{v_6} = \begin{pmatrix}5\\8\end{pmatrix}\), alors \(\overrightarrow{\Delta v}_5 = \begin{pmatrix}5-3\\8-7\end{pmatrix}=\begin{pmatrix}2\\1\end{pmatrix}\)
calcul du vecteur variation de vitesse|\[\overrightarrow{\Delta v}_i = \overrightarrow{v}_{i+1} - \overrightarrow{v}_i\]
méthode :
5 p. 224
exercice
En 2021, Devonte Graham, joueur des New Orleans Pelicans a marqué le plus long buzzer beater de tous les temps (18,6m)
assets/New_Orleans_Pelicans_Devonte_Graham_buzzer_beater.mp4
Voici une représentation de la trajectoire du ballon lors du shoot :
\(v_2 = \frac{M_1M_3}{2×Δt} = \frac{4,25}{2×0,2} = 10,6 \text{m.s}^{-1}\)

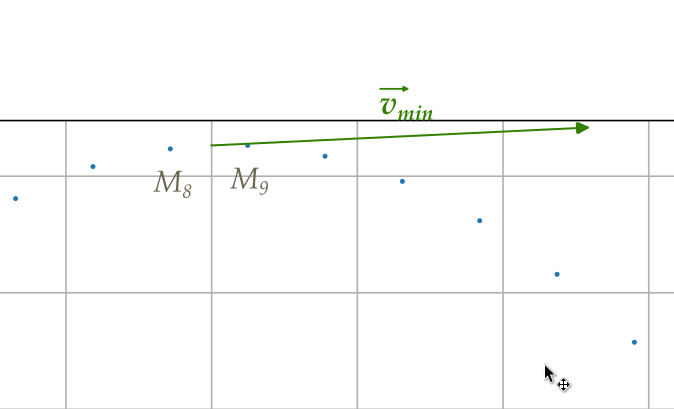
La vitesse est minimale entre M8 et M9.
\(v_\text{mini} = \frac{M_8M_9}{Δt} = \frac{1,3}{0,2} = 6,5\text{ m.s}^{-1}.\)
\(v_5 = \frac{M_4M_6}{Δt} = \frac{3,2}{0,4} = 8\text{ m.s}^{-1}.\)
\(v_6 = \frac{M_8M_9}{Δt} = \frac{3,0}{0,4} = 7,5\text{ m.s}^{-1}.\)
\(\overrightarrow{Δv}_{5\rightarrow 6} = \overrightarrow{v}_6 - \overrightarrow{v}_5\)
\(v_{10} = \frac{M_4M_6}{Δt} = \frac{2,75}{0,4} = 6,9\text{ m.s}^{-1}.\)
\(v_{12} = \frac{M_8M_9}{Δt} = \frac{3,1}{0,4} = 7,75\text{ m.s}^{-1}.\)
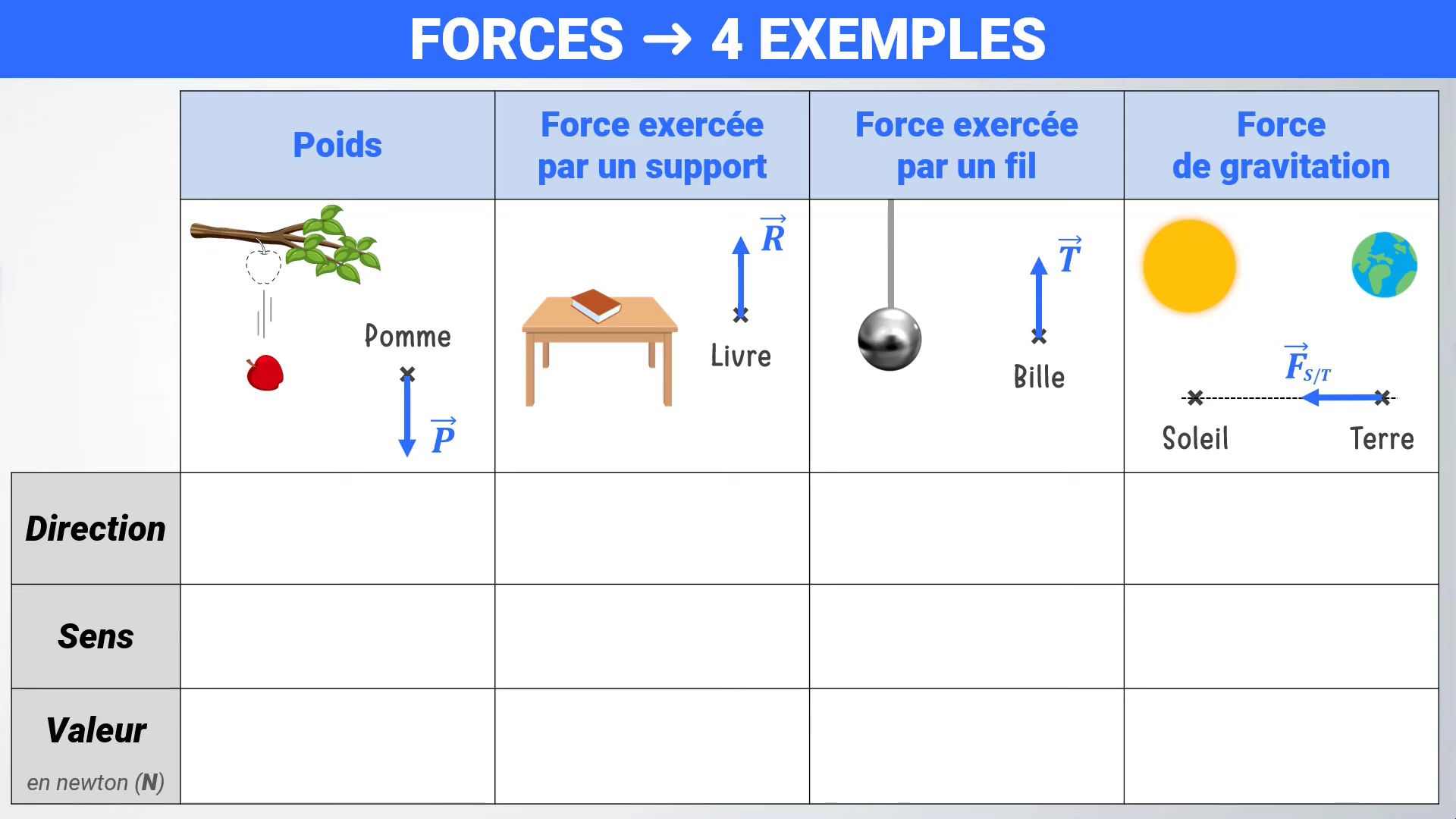
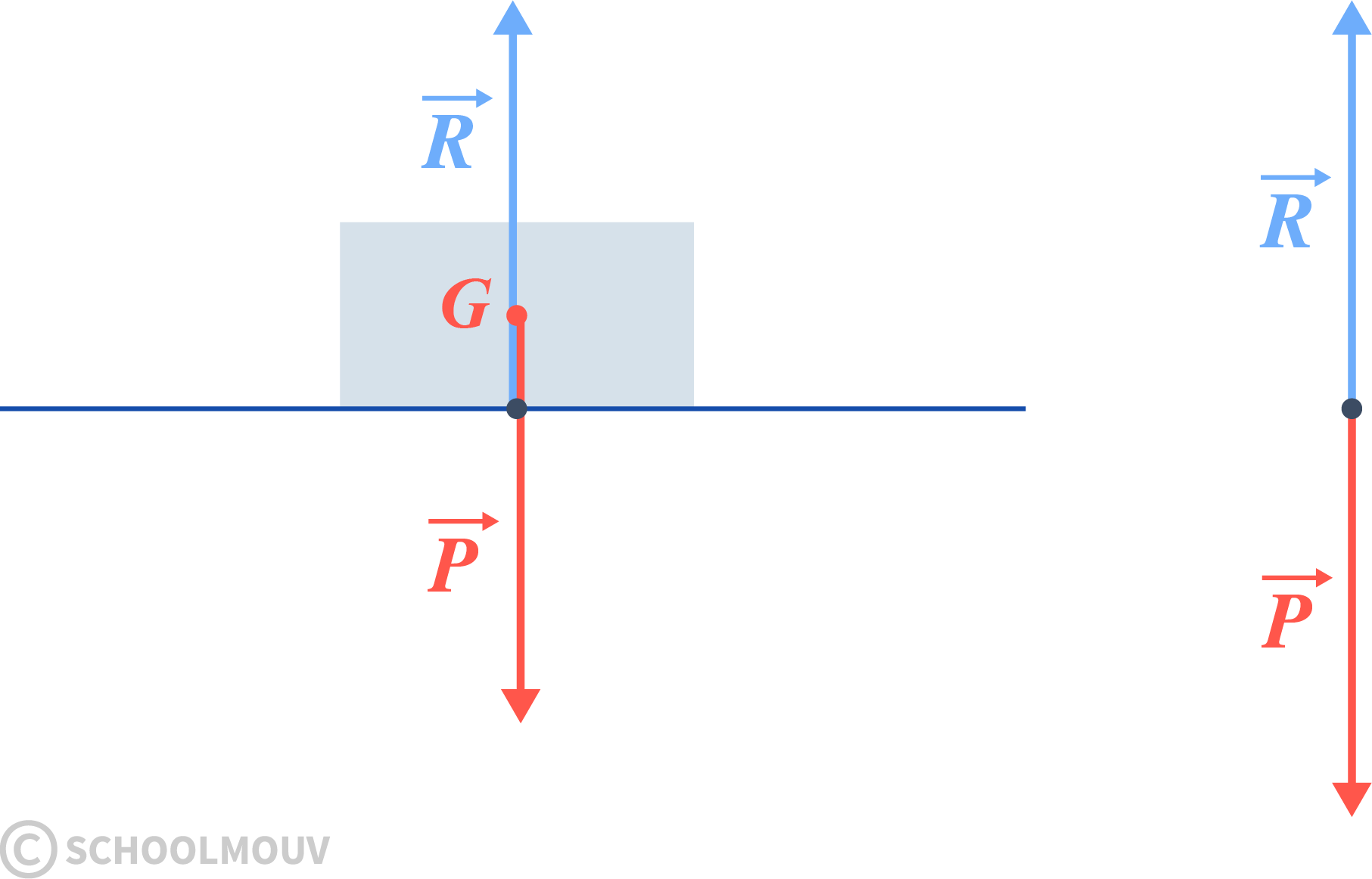
On définit \(\sum{\overrightarrow{F}}\) comme la somme des forces appliquées à l’objet étudié.
Principe fondamental de la dynamique : (ou 2e loi de Newton)
\[\frac{\overrightarrow{\Delta v}}{\Delta t} \approx \frac{\sum \overrightarrow{F}}{m}\]
L’accélération d’un objet M est proportionnelle à la somme des forces appliquées à cet objet divisé par la masse de l’objet.
N.B.1 − La relation devient égale lorsque l’intervalle \(Δt\) devient infiniment petit.
N.B.2 − On retrouve le principe d’inertie, lorsque \(\overrightarrow{F} = 0\), alors \(\overrightarrow{a}=\overrightarrow{0}\), le mouvement est rectiligne uniforme.
principe fondamental de la dynamique|\[\frac{\overrightarrow{\Delta v}}{\Delta t} \approx \frac{\sum \overrightarrow{F}}{m}\]