− déplacement ⟂ à la perturbation

− déplacement ∥ à la perturbation

Une onde progressive est une perturbation d’une grandeur physique qui se propage de proche en proche dans l’espace et au cours du temps. Une onde transporte de l’énergie mais ne déplace globalement pas de matière.
Une onde est dite mécanique si
elle a besoin d’un milieu matériel pour se propager.
exemples : ………………………………………………………………
Une onde est dite périodique si la perturbation se reproduit à l’identique à intervalles de temps réguliers.
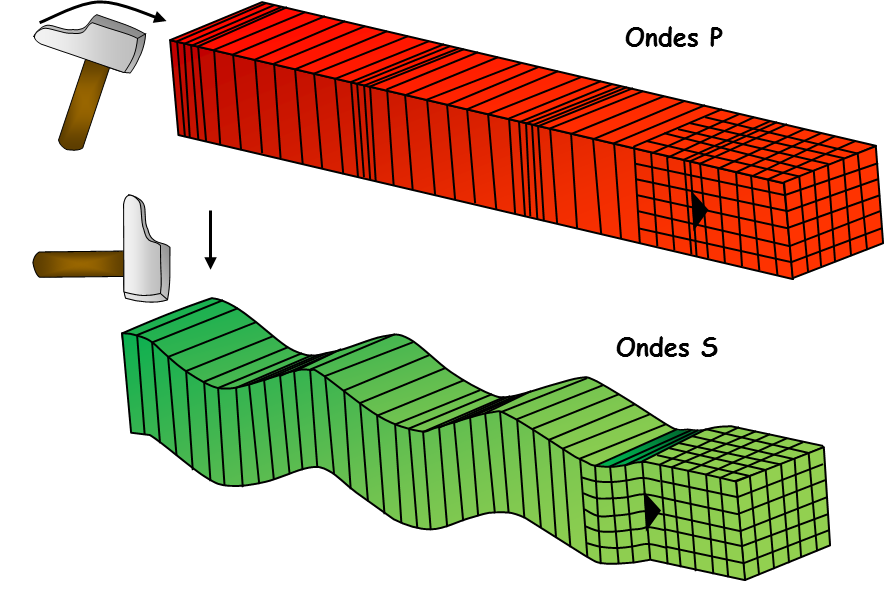
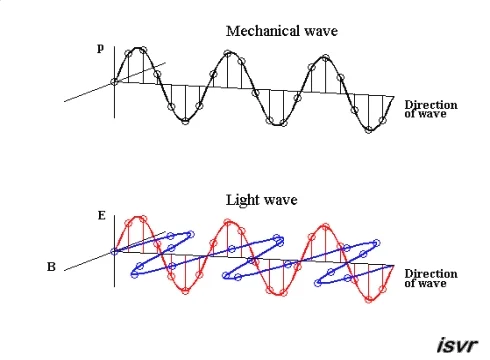
| onde transverse − déplacement ⟂ à la perturbation |
 |
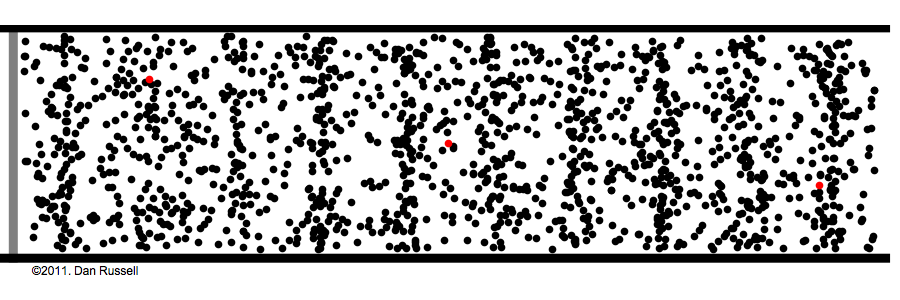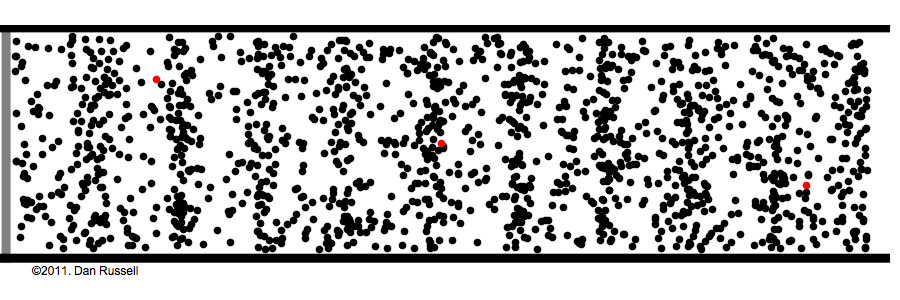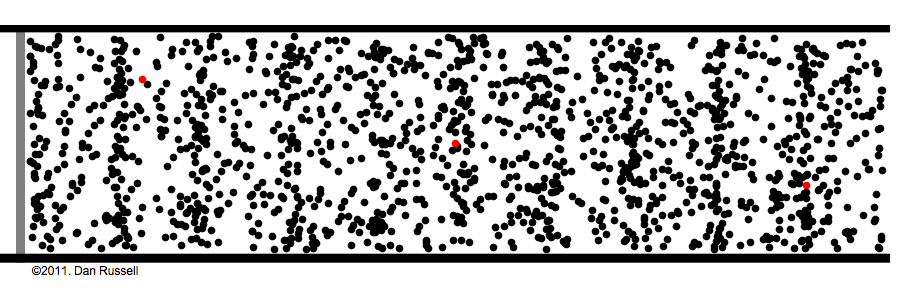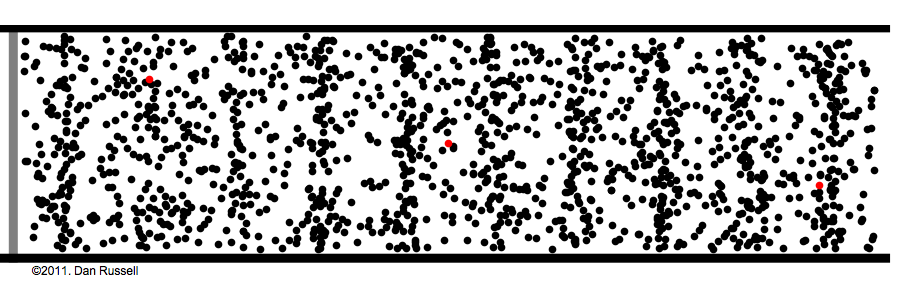
| onde longitudinale − déplacement ∥ à la perturbation |
 |
Ici \(τ = t_2 − t_1 \text{ avec } t_2 > t_1\)
notion de date et durée
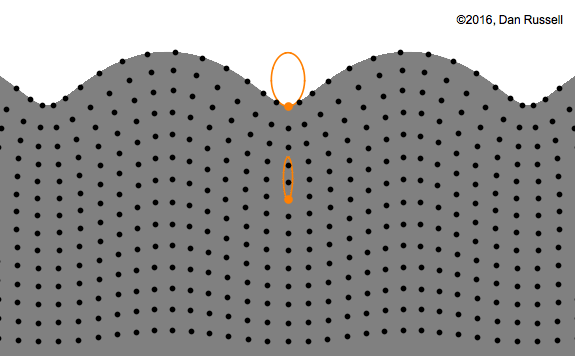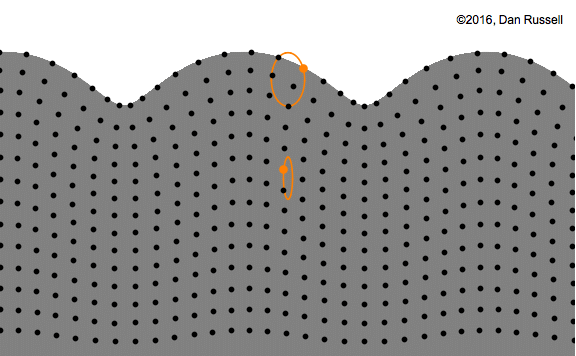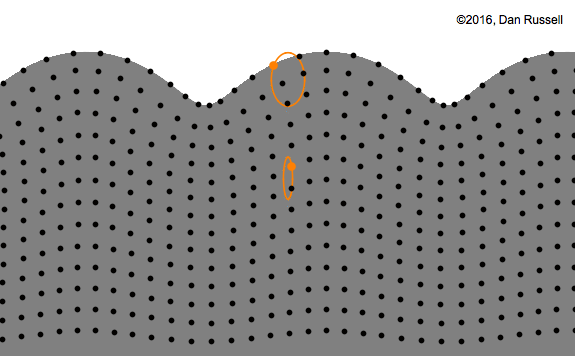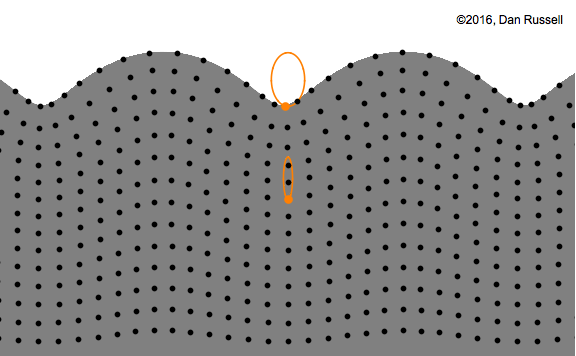
attention ici c’est une onde stationnaire, pas progressive
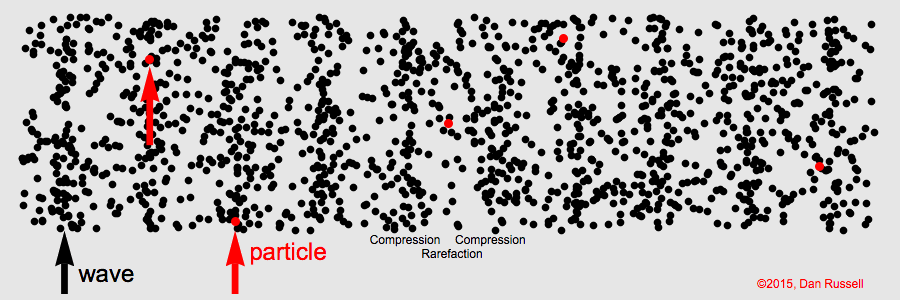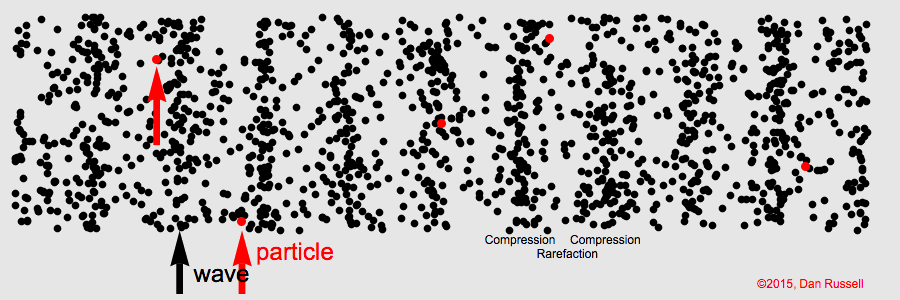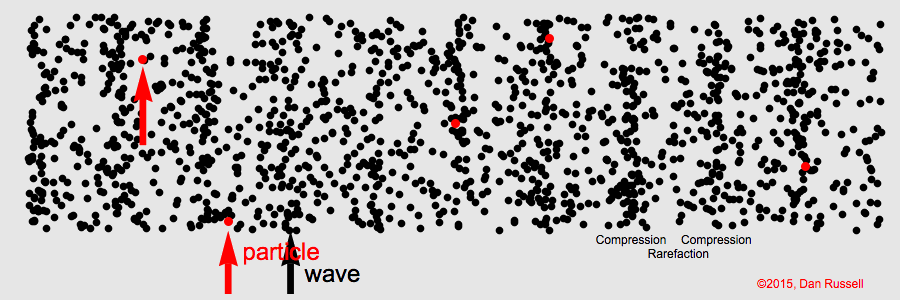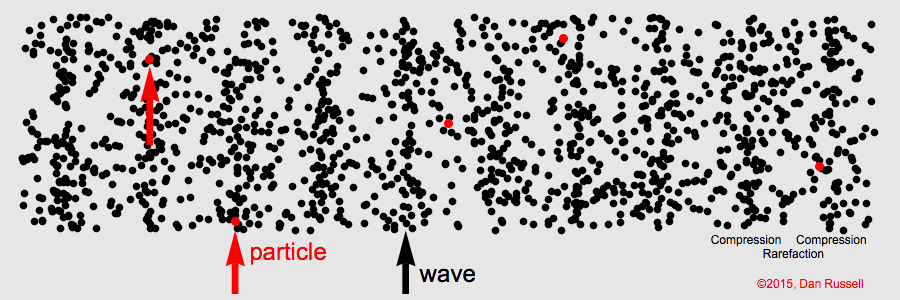

La célérité d’une onde est sa vitesse de propagation. Elle se calcule avec la relation :
|
\[v = \frac{AB}{τ}\] |
Avec :
|
En un point donné du milieu de propagation, la plus petite durée séparant deux états vibratoires identiques est appelée période (temporelle). Elle est notée T et se mesure en secondes.
La longueur d’onde (ou période spatiale) est la plus petite distance à partir de laquelle la forme de l’onde se répète. Elle est notée λ et se mesure en mètres. Elle dépend du milieu de propagation.
On peut représenter une onde de deux manières :
La fréquence f d’une onde périodique correspond au nombre de fois ou la perturbation se répète à l’identique par seconde. Elle s’exprime en Hertz (Hz) et on la calcule avec :
\[f = \frac{1}{T}\]
avec T : période temporelle en s
|
\[λ = c×T\] |
avec :
|
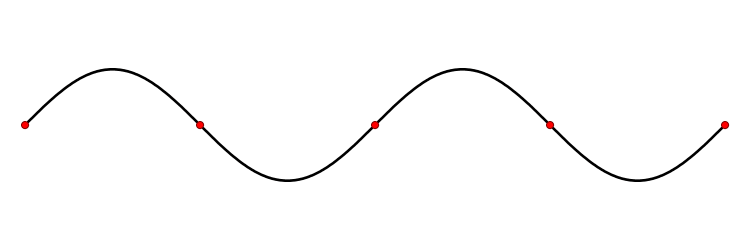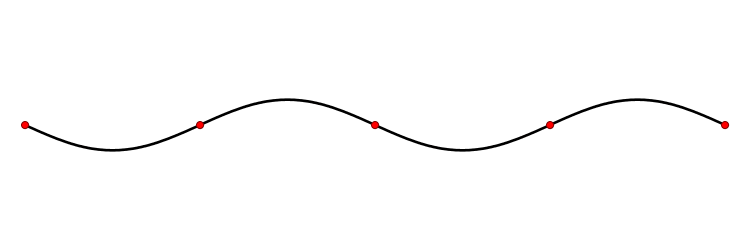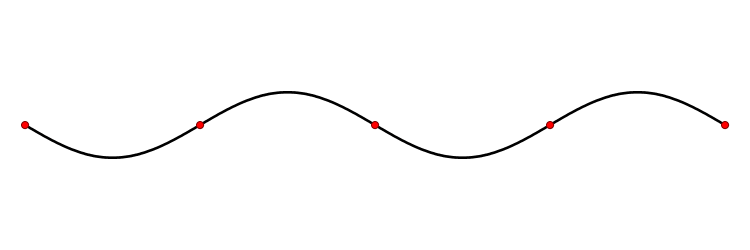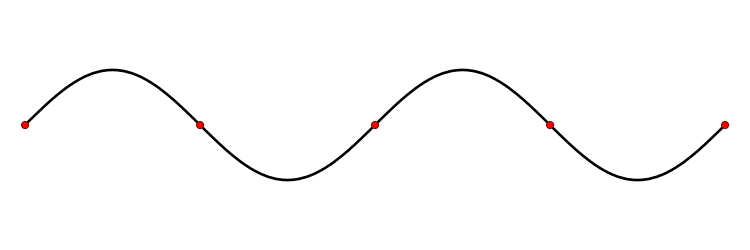
Quand la perturbation créée par la source est sinusoïdale, l’onde est qualifiée d’onde progressive sinusoïdale.
Son amplitude vaut :
\[A(t) = A×\sin(\frac{2\pi×t}{T} + φ)\]
\[A(x) = A×\sin(\frac{2\pi×x}{λ} + φ')\]
avec :
anim onde sin
expliquer que l’amplitude est une fonction à deux variables. Pour l’étudier on en fixe une.
On peut déterminer φ et φ’ en observant la valeur de la déformation pour une date connue (souvent t = 0 s).